Calculus III - Vector Fields

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 16.1 : Vector Fields

Back to Problem List

1. Sketch the vector field for \(\vec F\left( {x,y} \right) = 2x\,\vec i - 2\vec j\).

Show All Steps Hide All Steps

Start Solution

Recall that the graph of a vector field is simply sketching the vectors at specific points for a whole bunch of points. This makes sketching vector fields both simple and difficult. It is simple to compute the vectors and sketch them, but it is difficult to know just which points to pick and how many points to pick so we get a good sketch.

So, let’s start off with just computing some vectors at specific points.

\[\begin{align*} \vec F\left( {0, - 1} \right) & = - 2\vec j & \hspace{0.5in} \vec F\left( {1,1} \right) & = 2\,\vec i - 2\vec j & \hspace{0.5in} \vec F\left( { - 1,0} \right) & = - 2\,\vec i - 2\vec j\\ \vec F\left( { - 2, - 1} \right) & = - 4\,\vec i - 2\vec j & \hspace{0.5in} \vec F\left( {1, - 1} \right) & = 2\,\vec i - 2\vec j& \hspace{0.5in}\vec F\left( {2,2} \right) & = 4\,\vec i - 2\vec j\\ \vec F\left( { - 2,1} \right) & = - 4\,\vec i - 2\vec j\end{align*}\] Show Step 2

Now we need to “sketch” each of these vectors at the point that generated them. For example at the point \(\left( {0, - 1} \right)\) we’ll sketch the vector \( - 2\vec j\).

Here is the sketch of these vectors.

In the sketch above we didn’t sketch each of these vectors to scale. In other words we just sketched vectors in the same direction as the indicated vector rather than sketching the vector with “correct” magnitude. The reason for this is to keep the sketch a little easier to see. If we sketched all the vectors to scale we’d just see a mess of overlapping arrows that would be hard to really see what was going on.

Note as well that with the few vectors that we sketched it’s difficult to get a real feel for what is going on at any random point. With this sketch we might be able to see some trends but we don’t know that those trends will continue into “blank” regions that don’t have any vectors sketched in them.

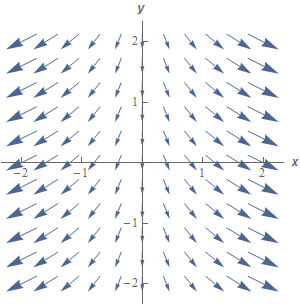
Show Step 3

Below is a better sketch of the vector field with many more vectors sketched in. We got this sketch by letting a computer just plot quite a few points by itself without actually picking any of them as we did in the previous step.

In general, this is how vector fields are sketched. Computing this number of vectors by hand would so time consuming that it just wouldn’t be worth it. Computers however can do all those computations very quickly and so we generally just let them do the sketch.