Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 16.2 : Line Integrals - Part I
For problems 1 – 7 evaluate the given line integral. Follow the direction of \(C\) as given in the problem statement.
- Evaluate \( \displaystyle \int\limits_{C}{{3{x^2} - 2y\,ds}}\) where \(C\) is the line segment from \(\left( {3,6} \right)\) to \(\left( {1, - 1} \right)\). Solution
- Evaluate \( \displaystyle \int\limits_{C}{{2y{x^2} - 4x\,ds}}\) where \(C\) is the lower half of the circle centered at the origin of radius 3 with clockwise rotation. Solution
- Evaluate \( \displaystyle \int\limits_{C}{{6x\,ds}}\) where \(C\) is the portion of \(y = {x^2}\) from \(x = - 1\) to \(x = 2\). The direction of \(C\) is in the direction of increasing \(x\). Solution
- Evaluate \( \displaystyle \int\limits_{C}{{xy - 4z\,ds}}\) where \(C\) is the line segment from \(\left( {1,1,0} \right)\) to \(\left( {2,3, - 2} \right)\). Solution
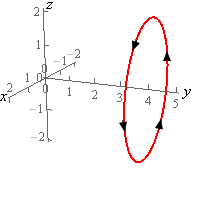
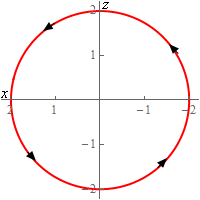
- Evaluate \( \displaystyle \int\limits_{C}{{{x^2}{y^2}\,ds}}\) where \(C\) is the circle centered at the origin of radius 2 centered on the \(y\)-axis at \(y = 4\). See the sketches below for orientation. Note the “odd” axis orientation on the 2D circle is intentionally that way to match the 3D axis the direction.
Solution
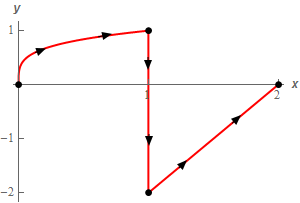
- Evaluate \( \displaystyle \int\limits_{C}{{16{y^5}\,ds}}\) where \(C\) is the portion of \(x = {y^4}\) from \(y = 0\) to \(y = 1\) followed by the line segment from \(\left( {1,1} \right)\) to \(\left( {1, - 2} \right)\) which in turn is followed by the line segment from \(\left( {1, - 2} \right)\) to \(\left( {2,0} \right)\). See the sketch below for the direction.
Solution
- Evaluate \( \displaystyle \int\limits_{C}{{4y - x\,ds}}\) where \(C\) is the upper portion of the circle centered at the origin of radius 3 from \(\displaystyle\left( {\frac{3}{{\sqrt 2 }},\frac{3}{{\sqrt 2 }}} \right)\) to \(\displaystyle\left( { - \frac{3}{{\sqrt 2 }}, - \frac{3}{{\sqrt 2 }}} \right)\) in the counter clockwise rotation followed by the line segment from \(\displaystyle\left( { - \frac{3}{{\sqrt 2 }}, - \frac{3}{{\sqrt 2 }}} \right)\) to \(\displaystyle\left( {4, - \frac{3}{{\sqrt 2 }}} \right)\) which in turn is followed by the line segment from \(\displaystyle\left( {4, - \frac{3}{{\sqrt 2 }}} \right)\) to \(\left( {4,4} \right)\).
See the sketch below for the direction.
Solution
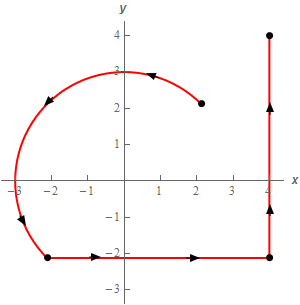
- Evaluate \( \displaystyle \int\limits_{C}{{{y^3} - {x^2}\,ds}}\) for each of the following curves.
- \(C\) is the line segment from \(\left( {3,6} \right)\) to \(\left( {0,0} \right)\) followed by the line segment from \(\left( {0,0} \right)\) to \(\left( {3, - 6} \right)\).
- \(C\) is the line segment from \(\left( {3,6} \right)\) to \(\left( {3, - 6} \right)\).
- Evaluate \( \displaystyle \int\limits_{C}{{4{x^2}\,ds}}\) for each of the following curves.
- \(C\) is the portion of the circle centered at the origin of radius 2 in the 1st quadrant rotating in the clockwise direction.
- \(C\) is the line segment from \(\left( {0,2} \right)\) to \(\left( {2,0} \right)\).
- Evaluate \( \displaystyle \int\limits_{C}{{2{x^3}\,ds}}\) for each of the following curves.
- \(C\) is the portion \(y = {x^3}\) from \(x = - 1\) to \(x = 2\).
- \(C\) is the portion \(y = {x^3}\) from \(x = 2\) to \(x = - 1\).