Calculus I - Minimum and Maximum Values (Practice Problems)

Show General Notice Show Mobile Notice Show All Notes Hide All Notes

General Notice

I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.

Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.

Paul
February 18, 2026

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 4.3 : Minimum and Maximum Values

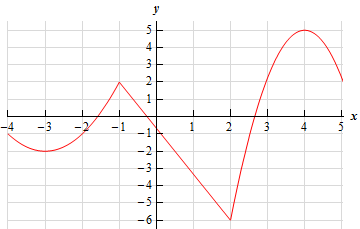
Below is the graph of some function, \(f\left( x \right)\). Identify all of the relative extrema and absolute extrema of the function.
Solution
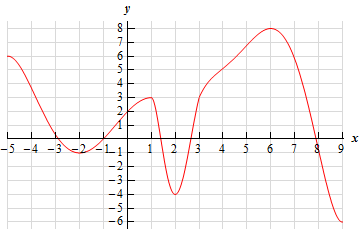
Below is the graph of some function, \(f\left( x \right)\). Identify all of the relative extrema and absolute extrema of the function.
Solution
Sketch the graph of \(g\left( x \right) = {x^2} - 4x\) and identify all the relative extrema and absolute extrema of the function on each of the following intervals.
1. \(\left( { - \infty ,\infty } \right)\)
2. \(\left[ { - 1,4} \right]\)
3. \(\left[ {1,3} \right]\)
4. \(\left[ {3,5} \right]\)
5. \(\left( { - 1,5} \right]\)
Solution
Sketch the graph of \(h\left( x \right) = - {\left( {x + 4} \right)^3}\)and identify all the relative extrema and absolute extrema of the function on each of the following intervals.
1. \(\left( { - \infty ,\infty } \right)\)
2. \(\left[ { - 5.5, - 2} \right]\)
3. \(\left[ { - 4, - 3} \right)\)
4. \(\left[ { - 4, - 3} \right]\)
Solution
Sketch the graph of some function on the interval \(\left[ {1,6} \right]\) that has an absolute maximum at \(x = 6\) and an absolute minimum at \(x = 3\). Solution
Sketch the graph of some function on the interval \(\left[ { - 4,3} \right]\) that has an absolute maximum at \(x = - 3\) and an absolute minimum at \(x = 2\). Solution
Sketch the graph of some function that meets the following conditions :
1. The function is continuous.
2. Has two relative minimums.
3. One of relative minimums is also an absolute minimum and the other relative minimum is not an absolute minimum.
4. Has one relative maximum.
5. Has no absolute maximum.
Solution